Space-efficient indexing for immutable log data

This post describes our approach to implementing a disk-backed hashmap in Rust for indexing high-cardinality predicates in our diagnostics product, Seq. If you've ever wondered how a hashmap works, or what makes a disk-backed datastructure different from an in-memory one, you might find it interesting.

Seq is a database for diagnostic events. It's designed to store large volumes of immutable event records with limited ingestion overhead. Records are initially ingested into unordered write-ahead-logs based on their timestamp. After some grace period has passed, multiple logs are sorted and coalesced into a single file covering some larger period of time. The start of every 4Kb page in that coalesced file is marked with a header pointing back to the start of the record that crosses its boundary. This scheme makes it possible to pick any random page in the file and hop forwards or backwards to the nearest record.

How indexing works in Seq

Like many other database systems, Seq maintains indexes to reduce the IO needed to serve a given query. Indexes are computed in the background after write-ahead-logs are coalesced. They store the set of pages in the coalesced file that contain the start of records matching some predicate in the query. Indexes can be treated like a bitmap, with bitwise union and intersection combining multiple indexes together. This page-based indexing scheme trades some query time for storage space. Diagnostic data is already high-volume, so we want to keep Seq's indexing storage requirements at just a few percent of the underlying data. Working at the page-level instead of the record-level means they store less data, but produce false-positives during querying. This is accounted for upstream by re-evaluating the query over all records in the read pages.

From low-cardinality to high-cardinality

Traditionally, Seq has stored indexes as bitmaps. Given a pre-defined predicate like Environment = 'Production', the index would evaluate the predicate over each record to produce a bitmap where pages containing any hits are set, and missed pages are unset. This works well for indexing low-cardinality properties like our Environment example, but isn't suitable for high-cardinality ones, like @TraceId. You can't predefine an index for trace and other correlation ids because you don't know the set of values in advance, and even if you did storing a bitmap for each would be suboptimal.

To support these high-cardinality cases, we made Seq's indexing scheme pluggable and implemented an additional approach for them. Instead of a bitmap, these indexes use a disk-backed hashmap we wrote that stores the hashes of values along with page hits for that particular value. Hit pages from the hashmap indexes are then fed back into Seq's retrieval pipeline in exactly the same way as bitmap indexes. That made it possible for us to focus our energy into designing the storage format for high-cardinality indexes without worrying about sweeping changes or specializations in the rest of the system.

A disk-backed hashmap for high-cardinality indexes

A hashmap can be implemented as an array of N buckets, where each bucket contains a set of (K, V) pairs:

type HashMap<K, V, const N: usize> = [Vec<(K, V)>; N];

The bucket to store a particular key in is determined by hashing it:

let bucket = hash(key) % N;

The contents of that bucket can then be scanned or searched to determine whether the key is present:

let existing = map[bucket].find_map(|(bucket_key, bucket_value)| if key == bucket_key {
    Some(bucket_value)
} else {
    None
});

Implementations like Rust's HashMap<K, V> are much more complicated than this, but even simple hashmaps are a great datastructure to reduce both insertion and lookup complexity by only operating on a bucket's worth of the map instead of the whole lot. This is the basic datastructure we used for our high-cardinality indexes.

Hashmaps aren't just great in-memory datastructures. They're great disk-backed datastructures too. An important property of a disk-backed datastructure is that its representation on-disk be the same as in-memory. That makes it possible to map a structure from a file and immediately use it without needing to buffer or deserialize the whole thing first. Working from disk however introduces the possibility of corruption either from bad storage, or manual tampering. Our implementation avoids many corruption issues by taking advantage of its write-once nature, and the system's tolerance of false positives. If a corruption is detected, instead of failing or attempting to recover, we can just return a set containing all pages in the file, suggesting every record needs to be re-evaluated.

With some idea of our requirements to minimize storage space, and constraints around false-positives, let's explore how the disk-backed hashmap is represented on disk. Everything it stores is a 32-bit integer. Instead of storing actual values in the map, a 32-bit hash is stored instead. Only storing hashes means all values have the same size, avoiding the need to also store lengths for them. Hash collisions are ok, because false-positives are allowed. The result of a collision will be a union of their respective hits.

At a high-level, the layout of the map looks like this:

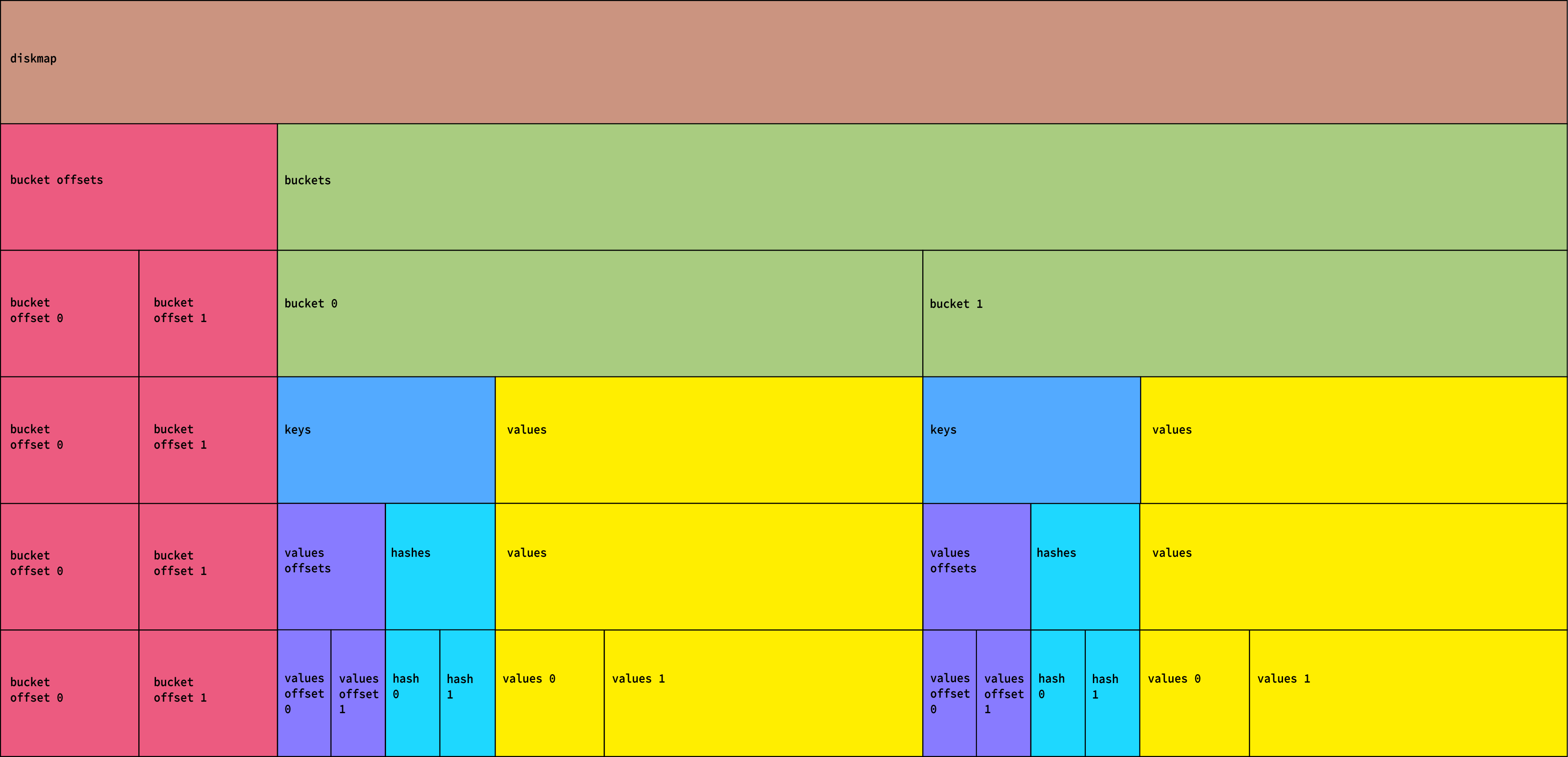
Let's break this diagram down from top to bottom.

diskmap: [ bucket offsets ][ buckets ]

The bucket offsets are a packed set of 32-bit integers:

bucket offsets: [ offset 0 ][ offset 1 ]..[ offset N ][ bucket 0 ][ bucket 1 ]..[ bucket N ]

Each offset is an offset in the map to the start of a bucket. That means the very first 32-bits in the map are the offset to the first bucket, which can also be interpreted as the length of offsets. We can tell by looking at this length how many buckets are in the map without needing to store that value explicitly. Where possible, we infer parameters from the map rather than store them directly for space efficiency.

Each bucket is itself split into two parts:

bucket: [ keys ][ values ]

The keys are two packed sets of hashes and values offsets:

keys: [ values offset 1 ]..[ values offset N ][ hash 1 ]..[ hash N ]

The values are a packed set of 32-bit hit pages in the indexed file.

Each hash value appears only once in keys, and has a corresponding pages offset pointing to its set of hit pages in values. We can tell how many hit pages there are for a given hash by looking at the pages offset of the next hash value. We can also infer how many keys are in the bucket by looking at the first pages offset.

Hash values are stored packed together so scanning a bucket for a matching hash can be vectorized. Once a match is found, its hit pages are also stored packed together and can be yielded directly.

The hashmap is built in-memory during background indexing and only formatted into its on-disk representation at the end. This means we can pick an optimal number of buckets for the map based on the number of values it contains. The bucket size we currently target is a single vector-width of hash values, so four on ARM with Neon, and eight on x86 with AVX2. Once the index is built, it can be read directly from disk without any further deserialization.

Let's look at an example of the raw hex bytes for a hashmap and work out what it's storing:

04000000 14000000 1C000000 01000000 02000000 02000000 01000000 01000000

The first four bytes are the offset to the first bucket:

04000000 == 4

That's also the length of the set of buckets. Each bucket offset occupies four bytes, so we can work out the number of buckets by dividing the offset to the first bucket by four: 4 / 4 == 1. There's one bucket in this map.

Looking at the 32-bit integer at the start of this bucket, we get:

14000000 == 20

That's the offset to the first page value. Each key in the map occupies eight bytes; four bytes for the offset to its values, and four bytes for its hash. We can work out the number of keys in the bucket by subtracting the bucket offset and dividing by eight: (20 - 4) / 8 == 2. There are two keys in this bucket.

Now we can split our bucket into its pages offsets, hashes, and values.

The pages offsets are:

14000000 1C000000 == 20, 28

The hashes are:

01000000 02000000 == 1, 2

The values are:

01000000 02000000 01000000 == 1, 2, 1

To find what values belong to what hash, we read the values between each of their pages offests.

The first hash, 1, contains the 32-bit integers between offset 20 and offset 28. That is:

01000000 02000000 == 1, 2

The second hash, 2, contains the 32-bit integers between offset 28 and the end of the bucket. That is:

01000000 == 1

So in the end, our map looks like:

{
    1: [1, 2],
    2: [1],
}

How our disk-backed hashmap compares

The disk-backed hashmap is essentially a HashMap<u32, HashSet<u32>>. To get an idea of the trade-offs at play, we roughly compare our implementation to two other approaches:

• diskmap: The disk-backed hashmap described in this post.
• odht: A disk-backed hashmap used in the Rust compiler. odht is in many ways a far more sophisticated project than our diskmap. It supports generic keys and values, but requires values have a fixed size. That makes it mostly unsuitable for our needs, but still an excellent project to explore.
• bincode: A regular in-memory HashMap<u32, HashSet<u32>>, serialized using bincode. It's not a disk-backed hashmap, but is the most straightforward approach you might consider when faced with needing to store a hashmap on disk. We've included it here to highlight the distinction between serialized and natively disk-based datastructures.

For this test, we're constructing a map containing 100,000 hash values, with 10 page hits for each.

Size on disk

Looking first at the size on-disk of the resulting maps, they're all within an order of magnitude, with diskmap using the least space:

odht   : 5,898,288 bytes
bincode: 5,200,008 bytes
diskmap: 4,850,000 bytes

We could further reduce size in each case with optimizations like variable-length integer encoding, but that would complicate reading.

Reading from an in-memory map

In this next case, we take an already in-memory representation of the hashmaps and read the key 561,388 from it. When it comes to reading values from a loaded hashmap, as expected the in-memory bincode map performs the best. At this point it's just a standard HashMap, which is already a very efficient datastructure in Rust. The important thing for us is that diskmap remains competitive:

diskmap: 159 ns/iter (+/- 12)
odht   : 102 ns/iter (+/- 6)
bincode:  24 ns/iter (+/- 1)

The advantage odht displays here is because it supports a fixed number of values per key; diskmap incurs some additional overhead because each key can be mapped to any number of values, which is important in our scenario.

Reading directly from disk

The final case is the same as the previous one, except we also pay the cost of converting from the on-disk into the in-memory representation. This is the main use-case for Seq's indexing. Instead of keeping indexes resident in-memory, we memory map them on-demand, relying on the OS's page cache to keep fragments of them warm if they're frequently used.

Both diskmap and odht are able to operate off the raw on-disk bytes with no deserialization step needed. Both can be memory-mapped from a file and used as-is whereas the bincode implementation needs to be decoded using bincode before it can be used.

bincode: 7,595,600 ns/iter (+/- 1,041,337)
diskmap:       161 ns/iter (+/- 19)
odht:          107 ns/iter (+/- 6)

Exploring the source

We wrote our own disk-backed hashmap to support high-cardinality indexing in Seq. It forms part of a pluggable indexing scheme, so we can continue developing new approaches in the future for differently shaped indexing problems. It was a lot of fun to write, the implementation satisfies our requirements for both storage and read efficiency, and best of all, it fits comfortably in a single file. You can explore the source yourself here on GitHub.